【G-2】xb記法
目次
(´･ω･ ｀)<ほいだら、続きをやるかの。
( ﾟдﾟ)<うい。何やったっけ？
(´･ω･ ｀)<もう忘れたんかいな。
( ﾟдﾟ)<そらあそういうこともあるがな。誰だってそうや。きみもそうやろ？
(´･ω･ ｀)<まあ、そういうこともあるけどさ。
( ﾟдﾟ)<な？ほいだらさっさと複数の人や組織の一連の取引を第三者の視点から記述する方法ってのを説明しんさい。
(´･ω･ ｀)<だいぶちゃんと覚えとるやんけ。
前回の復習
まずは前回の復習から始めましょう。
「商社Aが仕入先のBから100円で商品を仕入れた。そして、その商品を顧客であるCに150円で売った。」
この取引におけるAの仕訳はこのように↓なります。
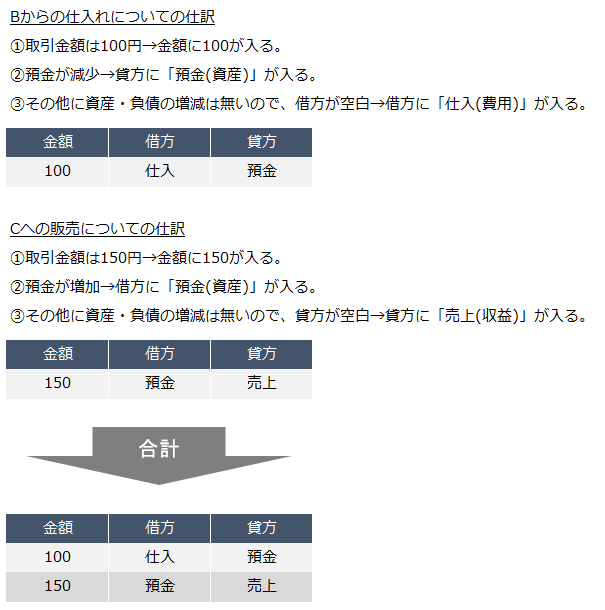いかがでしょうか。分からなかった方は前回記事の【G-1】を再読いただければと思います。
xb記法とは
さて、もしも私たちの目的がAの帳簿作りなのであれば、話はここでおしまいです。
がしかし、当ブログの趣旨はそういうことではありません。マクロ経済つまり世の中全体の経済の仕組みを理解しようというものです。
そこで、Aだけではなくて、仕入先B・顧客Cのことも含めて「全体としてはどうなっているのか」を考える必要が出てきます。
つまりはこの4つ↓の仕訳をまとめて全部いっぺんに考えたいわけです。
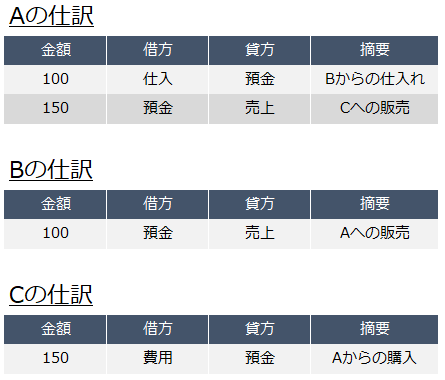
しかし、このように単に仕訳を並べるだけだと、たったこれだけの取引量ですら「全体がどうなっているのか」をイメージするのはちょっとしんどいものがあります。
そこで、もう一歩進んだ「複数の会計主体による取引の全体をまとめて示せる記述法」が必要になってきます。なお、《会計主体》とはこのときのAやBやCのことです。
xb記法の書き方
この問題に対して私が「こうしたらいいんじゃなかろうか」と考え出したのが、こういう↓書き方です。なお、金額については以降無視します。
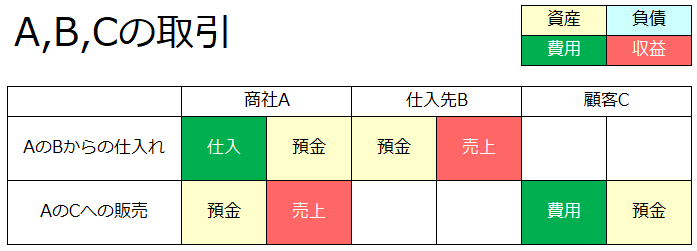
この書き方であれば、全体の動きをまとめて把握することができます。名前が無いのはいささか不便なので、僭越ながら、これを「xb記法」と呼ぶことにします。
ストック科目とフロー科目
ここで《ストック科目》と《フロー科目》という2つのワードを追加しておきます。
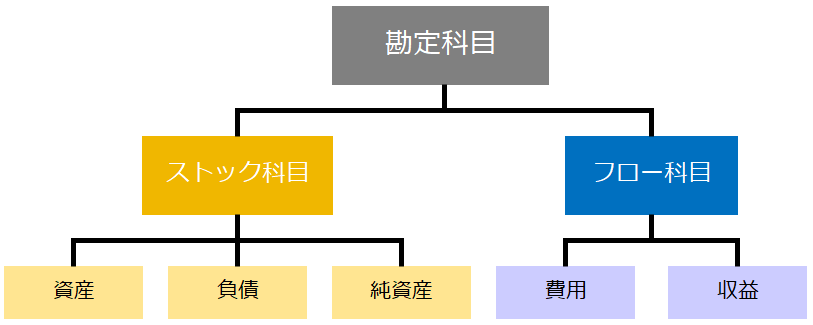
【G-1】のとおり、全ての勘定科目は資産・負債・純資産・費用・収益の5つのグループのどれかに区分されます。
そのうち、資産・負債・純資産に区分されている科目が「ストック科目」で、費用・収益に区分されている科目が「フロー科目」です。
科目の相殺消去
xb記法で各主体の仕訳の合計を示すときは、次の2パターンに当てはまる箇所があれば、できるだけ相殺消去をして示すことにします。
- ストック科目については、借方と貸方に同じ科目が1つずつあるとき
- フロー科目については、借方と貸方に費用と収益が1つずつあるとき
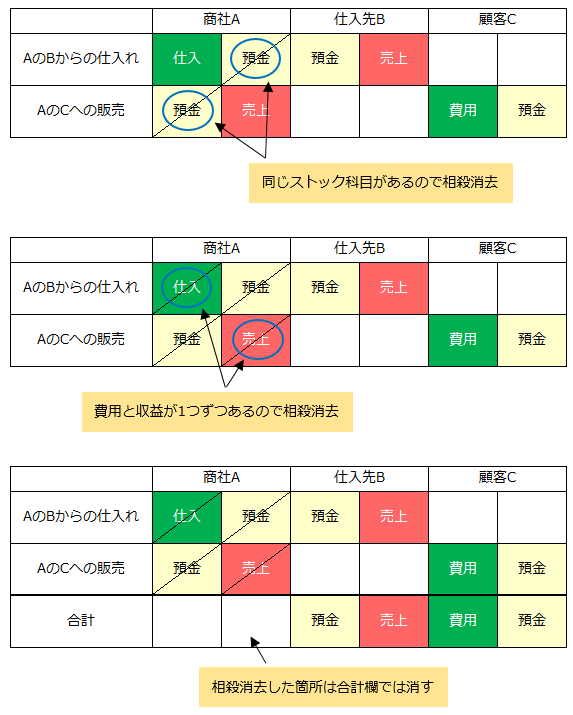
なお、この相殺消去は単純に見やすくするための処置です。別に「これをやらないと、仕訳が成り立たなくなる」とか、そういった実際上の問題が起こるわけではありません。
ですが、相殺消去をした方が見やすいので、当ブログでは、消せるものは出来るだけ消すようにします。
横断合計ゼロ法則
さて、上記の各主体の仕訳の合計は、言わば「縦方向の合計」です。
xb記法の利点は何と言っても、複数の会計主体の仕訳を横断的に一覧できることですので、今度は「横方向の合計」についても考えてみましょう。
つまり、最初に示したA,B,Cの仕訳について、1行目のAとB、2行目のAとCの仕訳をまとめて1つのものとして考える、ということをやってみるわけです。
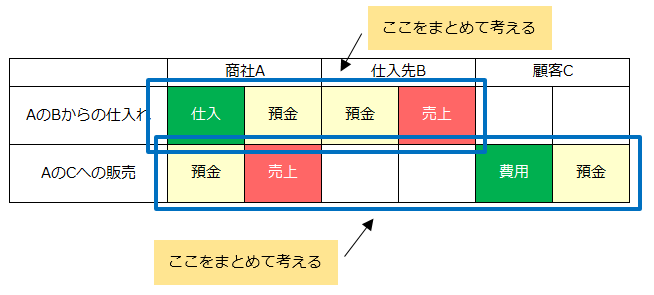
以下、この複数の会計主体の仕訳をまとめて1つのものと考えたときの1行目・2行目のことを《横断仕訳》と呼ぶことにします。
横断合計における科目の相殺消去
ここでも縦方向の合計のときと同じように相殺消去を考えてみます。但し、こちらはストック科目について少しだけ対象が広がります
- ストック科目については、借方と貸方に同じ科目(例:現金-現金)または対となる科目(例:貸付金-借入金)が1つずつあるとき
- フロー科目については、借方と貸方に費用と収益が1つずつあるとき
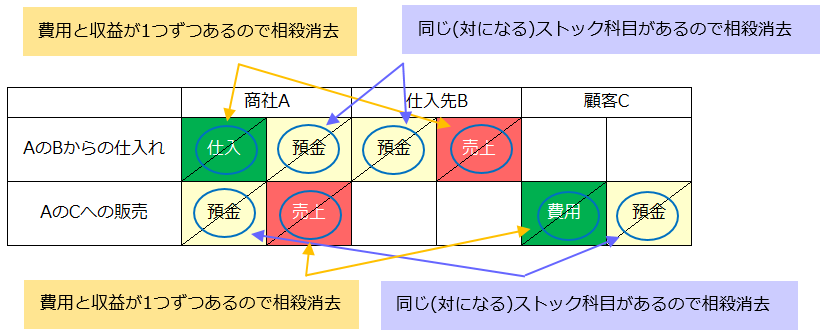
すると、1行目の横断仕訳も、2行目の横断仕訳も全ての科目が相殺消去されることになります。
これは偶然ではありません。
どんな取引の横断仕訳であっても、上記のルールで相殺できるものを全て相殺していくと必ず最後には全ての科目が消去されることになります。
つまり、横断仕訳の中の各仕訳を全て足し合わせた合計は、それがどんなに複雑な取引であっても、必ずゼロになります。
例えば銀行間振込は、
- 振込みをする人
- 振込み元の銀行
- 日本銀行
- 振込み先の銀行
- 振込みを受ける人
という五者が関連する複雑な取引ですが、やはり横断仕訳の合計はゼロになります。
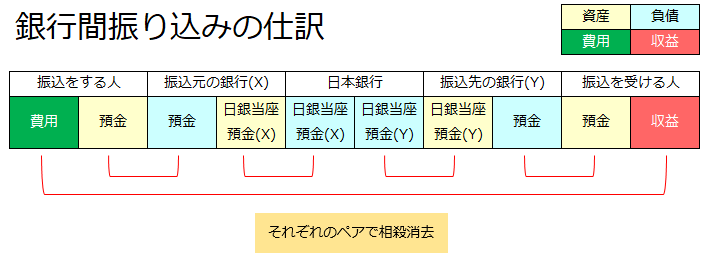
今は仕訳自体の意味まで理解する必要はありません。合計がゼロになることだけ確認してもらえればOKです。
こちらも名前が無いのは不便ですので、上記の法則のことを《横断合計ゼロ法則》と呼ぶことにします。
なぜ横断合計はゼロになるのか
さて、横断合計ゼロ法則はなぜ成り立つのでしょうか。
もちろんxb記法だから成り立つ、ということではありません。xb記法は単なる表現方法の工夫ですので、xb記法で書くかどうかによって取引の内容が変化することは無いからです。
それでは以下で横断合計ゼロ法則が成り立つ理由を説明していきましょう。
二者間取引の横断合計はゼロになる
まず、あらゆる二者間取引の横断合計はゼロになることを示します。
ただ、"あらゆる"とは言っても、実際のところ、二者間取引のパターンは、基本的には次の2つしかありません。
- 資産を渡す(受け取る)取引
- 負債を発行する(受け取る)取引
これに費用・収益の発生を伴うパターンも加えるとパターンは3つとなります。
なお、純資産は「資産と負債の差額」ですので、これは渡したり受け取ったりするものではありませんから、「純資産を渡す(受け取る)取引」というパターンはありません。
同様に、「費用を渡す(受け取る)取引」や「収益を渡す(受け取る)取引」というパターンもありません。
資産受け渡し取引の横断合計
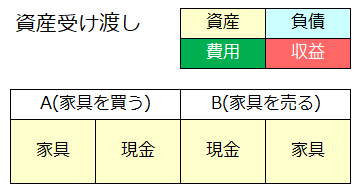
まずは資産を渡す(受け取る)取引を考えてみます。例えば、「AがBから現金(資産)で家具(資産)を買う」という取引です。
- Aは家具(資産)を得て、現金(資産)を減らした。
- Bは現金(資産)を得て、家具(資産)を減らした。
ということですので、この取引の仕訳はこう↓なります。
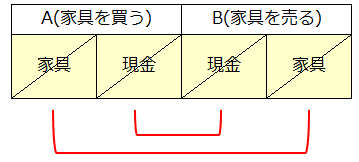
- Aの貸方・Bの借方に同じ資産(=現金)があるので相殺消去できる。
- Aの借方・Bの貸方にも同じ資産(=家具)があるので、これも相殺消去できる。
よって、この取引の横断合計はゼロです。
負債受け渡し取引の横断合計
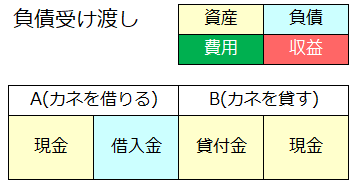
続いて負債を発行する(受け取る)取引を考えてみます。例えば、「AがBから現金(資産)を借りて、借用書を書いて渡した。」という取引です。
ここで、借用書の存在はAにとっては「カネを借りた」という事実であり、Bにとっては「カネを貸した」という事実ですから、Aが計上するのは「借入金(負債)」であり、Bが計上するのは「貸付金(資産)」と科目が異なることに注意してください。
つまり、
- Aは現金(資産)を増やして、借入金(負債)を増やした。
- Bは貸付金(資産)を増やして、現金(資産)を減らした。
ということですので、この取引の仕訳はこう↓なります。
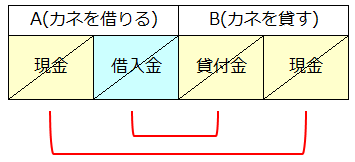
- Aの貸方には「借入金(負債)」が、Bの借方には「貸付金(資産)」があり、この2つは対になっているので相殺消去できる。
- Aの借方・Bの貸方に同じ資産(=現金)があるので、これも相殺消去できる。
よって、この取引の横断合計もゼロです。
費用・収益の発生を伴う取引の横断合計
最後に費用・収益の発生を伴うパターンを考えてみます。例えば、「AがBに借金の利息として現金を支払う」という取引です。
この取引では、AがBへ現金を単に渡すだけですので、
- Aは現金(資産)を減らした。
- Bは現金(資産)を増やした。
ということになります。いったんこのような↓仕訳を書いておきましょう。
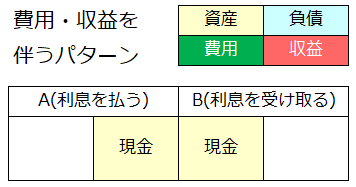
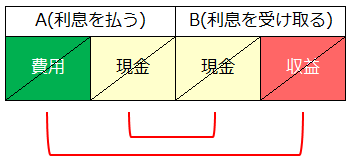
Aの借方とBの貸方が空白ですので、Aの借方に費用を、Bの貸方に収益を入れて仕訳が完成します。
- Aの貸方・Bの借方に同じ資産(=現金)があるので相殺消去できる。
- Aの借方の費用・Bの貸方の収益も相殺消去できる。
よって、この取引の横断合計もやはりゼロです。
二者間の横断合計に関するまとめ
つまり、
- 資産受け渡し取引の横断合計はゼロである。
- 負債受け渡し取引の横断合計はゼロである。
- 費用・収益の発生が伴う取引の横断合計はゼロである。
ということですから、二者間取引は全てのパターンにおいて横断合計がゼロになることが分かります。
これは、
- 資産の受け渡しは資産が移動しただけだから、全体としての変化は無い。
- 発行された負債は受け取り側にとっては資産なので、対になる資産の発生を必ず伴う。
と考えれば、当然のことと理解できるかと思いますし、また、費用・収益を伴う取引については、
- A-Bの二者間取引でAが収益を得たということは、
- Aが「資産を増やした」または「負債を減らした」ということなので、
- それは一方でBが「資産を減らした」または「負債を増やした」ということであり、
- それはBが費用を計上するということである。
- つまり、Aが収益を得れば、Bは必ず費用を計上することになる。
と考えれば、これも理解できると思います。
全ての取引は二者間取引の重ね合わせ
続いて、実はあらゆる取引は複数の単純な二者間取引に分解することができます。
銀行間振込の仕訳は先述のとおり複雑なものですが、
これも4つの単純な二者間取引に分解することが可能であり、上記の仕訳はそれらを重ね合わせて縦方向の相殺消去をしたものです。
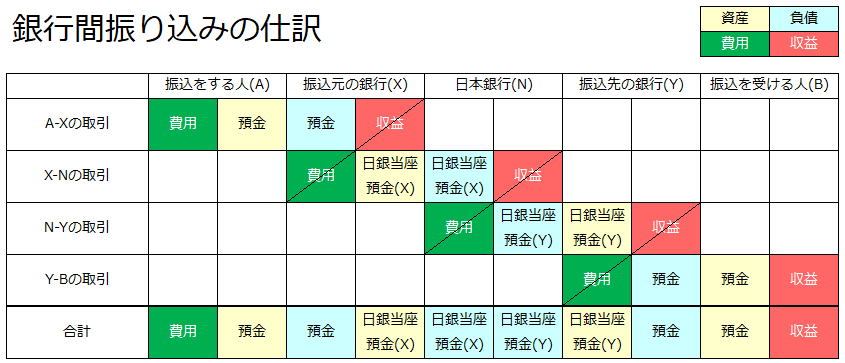
分解した個別の仕訳についても現段階では仕訳の意味まで理解する必要はありません。見ていただきたいのは4つの二者間取引の仕訳の重ね合わせが元の仕訳と同じになっていることです。
横断合計ゼロ法則が成り立つ理由のまとめ
- 全ての二者間取引の横断合計はゼロになる。
- 全ての取引は二者間取引の重ね合わせである。
ゼロにいくらゼロを重ね合わせても、その合計はもちろんゼロになります。
であるからして、全ての取引の横断合計はゼロになるというわけです。
横断合計ゼロ法則の応用
「全ての取引は横断合計はゼロになる」ということは、「ある仕訳が取引の内容を正しく記述したものであるならば、その横断合計は必ずゼロになる」ということです。
そして、ある命題が真ならばその対偶も真です。
よって、「ある仕訳の横断合計がゼロにならなければ、それは取引の内容を正しく記述したものではない」という命題も導き出すことができます。
私は経理業務をやっているときにこの知識をよく使います。自分の切った仕訳が正解かどうかをチェックしたいときは、その取引に関連する全ての会計主体の仕訳を考えてみて、その横断合計を求めてみればよいのです。
横断合計を求めて、それがゼロにならなかったら、自分の仕訳は間違いだと分かります。
もしかしたら簿記検定の試験でも使えるテクニックなのかもしれません。なお、ゼロになったからと言って必ずしも正解であるとは限らないことには注意してください。
次回予告
(´･ω･ ｀)<うし、ここまでで簿記の説明はおしまいや。おつかれさん。
( ﾟдﾟ)<うい。おつかれさん。ほいだら次からMMT解説の本編スタートか？
(´･ω･ ｀)<うんにゃ。まだあと1つ説明しとかなあかんことがあるんよ。
( ﾟдﾟ)<ほう、と言いますと？
(´･ω･ ｀)<B払いや。
( ﾟдﾟ)<なんやそれ。しばくぞ。
(´･ω･ ｀)<しばくな。短気か。
( ﾟдﾟ)<おう、そこそこな。
(´･ω･ ｀)<困ったやっちゃの。
( ﾟдﾟ)<おう、そこそこな。
(´･ω･ ｀)<んーと、B払いは一言で説明するのはちょっと難しいんやけど、複式簿記とこれは覚えといてもらわんとMMTの説明はなかなかしんどくての。今日のところはとりあえず名前だけっちゅうことで。
( ﾟдﾟ)<ういー。
それでは本日ここまで。
おまけ
遅ればせながら、あけましておめでとうございます。今年初の更新になりました。本年もどうぞよろしくお願いいたします。
今後もこんな感じで、だいたい毎月後半に、月1くらいの更新になると思います。
さて、それでは皆さん気になってると思いますので、最近の私の朝ごはんの定番を公開しようと思います。
こちらです。どん。
最近は週末にこの動画の食べるラー油を作り置きしといて、平日の朝に卵かけご飯に乗っけて食ってます。いや、もうね、実にうまい。
よろしければお試しください。
日本人は本当はもっと豊かになれます。そのためにはもっと多くの人々が貨幣と経済の仕組みを理解しなければなりません。
私たちが、そして次世代の子供たちが、貧困に怯えずに暮らせる日本を目指しましょう。
( ﾟдﾟ)<最後まで読んでいただき、ありがとうございます！！！
応援コメント、指摘コメント、お待ちしております！当ブログの拡散も大歓迎です！
よろしくお願いします！
